วันจันทร์ที่ 20 กรกฎาคม พ.ศ. 2558

แคลคูลัส


เขียนโดย ที่ ไม่มีความคิดเห็น:

การหาลิมิต

ในวิชาคณิตศาสตร์ ลิมิตของฟังก์ชัน เป็นแนวคิดพื้นฐานของ คณิตวิเคราะห์ (ภาคทฤษฎีของแคลคูลัส)
ถ้าเราพูดว่า ฟังก์ชัน f มีลิมิต L ที่จุด p หมายความว่า ผลลัพธ์ของ f จะเข้าใกล้ L ที่จุดใกล้จุด p สำหรับนิยามอย่างเป็นทางการนั้น มีการกำหนดขึ้นครั้งแรก ช่วงปลายของคริสต์ศตวรรษที่ 19 มีรายละเอียดอยู่ข้างล่าง


นิยามเป็นทางการ[แก้]

ฟังก์ชันบนปริภูมิอิงระยะทาง[แก้]

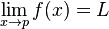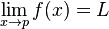กำหนดให้ f : (M,dM) -> (N,dN) เป็นการส่งค่าระหว่าง (เป็นฟังก์ชันที่นิยามบน) ปริภูมิอิงระยะทาง สองปริภูมิ, และกำหนดให้ p ∈M และ L ∈N, เราจะกล่าวว่า "ลิมิตของ f ที่ p คือ L" และเขียนว่า: \lim_{x \to p}f(x) = L ก็ต่อเมื่อ สำหรับทุกค่าของ ε > 0 จะมี δ > 0 ที่ สำหรับทุกๆ x ∈M และ dM(x, p) < δ แล้ว, dN(f(x), L) < ε

ฟังก์ชันค่าจริง[แก้]

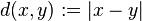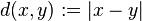เซตของจำนวนจริงหรือเส้นจำนวนจริง โดยทั่วไปสามารถมองเป็นปริภูมิอิงระยะทางได้ โดยมี d(x, y) := |x-y|. เช่นเดียวกับ เส้นจำนวนจริงขยาย (เส้นจำนวนจริงที่เพิ่ม +∞ และ -∞ เข้าไปด้วย) ก็สามารถมองเป็นปริภูมิอิงระยะทางได้ โดยมี d(x, y) := |arctan(x)-arctan(y)|

ลิมิตของฟังก์ชันค่าจริงที่จุดใดจุดหนึ่ง[แก้]

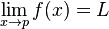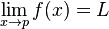ให้ f เป็นฟังก์ชันค่าจริง แล้วเราจะเขียน  \lim_{x \to p}f(x) = L  ก็ต่อเมื่อ สำหรับทุกค่าของ ε > 0 (ไม่ว่าจะเล็กเท่าใด) จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, |f(x)-L| < ε
ซึ่งเป็นกรณีพิเศษของฟังก์ชันบนปริภูมิอิงระยะทาง ที่มีทั้ง M และ N เป็นเซตของจำนวนจริง และ d(x,y) = |x-y|.
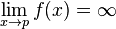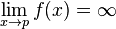หรือเราจะเขียน  \lim_{x \to p}f(x) = \infty ก็ต่อเมื่อ สำหรับทุกค่าของ R > 0 (ไม่ว่าจะใหญ่เท่าใด) จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, f(x) > R;
หรือจะเขียนว่า  \lim_{x \to p}f(x) = -\infty ก็ต่อเมื่อ สำหรับทุกค่าของ R < 0 จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, f(x) < R.
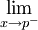
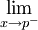
ถ้าในนิยาม เราใช้ x-p แทน |x-p| เราก็จะได้ ลิมิตขวา เขียนแทนโดย : \lim_{x \to p^+} และถ้าใช้ p-x แทน ก็จะได้ ลิมิตซ้าย เขียนแทนโดย : \lim_{x \to p^-}

ลิมิตของฟังก์ชันค่าจริง ณ อนันต์[แก้]

จะมีลิมิตของฟังก์ชัน ณ อนันต์ ถ้า สำหรับ ε > 0 ใดๆ มี S > 0 อย่างน้อยหนึ่งค่า ที่ทำให้ |f(x)-L| < ε สำหรับ x > S ใดๆ
ให้ f(x) เป็นฟังก์ชันค่าจริง เราจะพิจารณาลิมิตของฟังก์ชันเมื่อ x เพิ่มขึ้น หรือลดลงอย่างไม่มีที่สิ้นสุด
เราจะเขียน
\lim_{x \to \infty}f(x) = L

ฟังก์ชันค่าเชิงซ้อน[แก้]

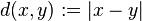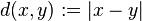ระนาบเชิงซ้อน ที่มีตัววัด (metric) เป็น d(x, y) := |x-y| จะเป็นปริภูมิอิงระยะทาง (metric space) ด้วยเช่นกัน จะมีลิมิตสองประเภทเมื่อเราพูดถึงฟังก์ชันค่าเชิงซ้อน

ลิมิตของฟังก์ชันที่จุดใดจุดหนึ่ง[แก้]

สมมติให้ f เป็นฟังก์ชันค่าเชิงซ้อน แล้วเราจะเขียนว่า
\lim_{x \to p}f(x) = L
ได้ ก็ต่อเมื่อ
สำหรับ ε > 0 ใดๆ จะมี δ >0 อย่างน้อย 1 ค่า ซึ่งสำหรับจำนวนจริง x ใดๆ ซึ่ง 0<|x-p|<δ จะได้ |f(x)-L|<ε
นี่เป็นกรณีพิเศษของฟังก์ชันบนปริภูมิอิงระยะทางที่มีทั้ง M และ N เป็นระนาบเชิงซ้อน

ลิมิตของฟังก์ชัน ณ อนันต์[แก้]

เราจะเขียน
\lim_{x \to \infty}f(x) = L
ได้ ก็ต่อเมื่อ
สำหรับ ε > 0 ใดๆ จะมี S >0 ซึ่งสำหรับจำนวนเชิงซ้อน |x|>S ใดๆ เราจะได้ |f(x)-L|<ε




เขียนโดย ที่ ไม่มีความคิดเห็น:
สมัครสมาชิก: บทความ (Atom)